数学¶
拓扑学¶
\(R^m\) 的子集 \(X\) 的一种性质叫做拓扑性质,如果它等介于一个只利用:math:X 的开集的概念与集合论的一些标准既来下定义的性质。
主要研究存在性定理,例如大多数应用的共同特点出现在一个存在定理的证明中,一个存在定理是这样的定理,它断言,某一个大类问题中的每一个,有某种特殊性质的的一个解。 存在定理是拓扑学的基本结构。
主要定理的应用,关于多项式的零点,映射的不动点以及向量场的奇点等的存在定理。也要用于证明紧致性,连通性以及连续性。
拓扑学定义¶
\(R^m\) 的子集 \(X\) 的一种性质叫做拓扑性质,如果它等价于一个只利用 \(X\) 的开集的概念与集合论的一些标准概念(元素,子集,补集,并集,交集,有限集,无限集等等)来定义的性质,简短的说 \(R^m\) 的子集X 的拓扑性质就是可以表达X的开集族的性质的那一种性质。
\(R^m\) 的子集`X`与 \(R^n\) 的子集 Y 叫做拓扑等价(或者同胚),如果存在一个一对一的函数 \(f:X->Y\) 使得 f 连续并且 \(f^{-1}:Y-X\) 也连续,此外,这函数f叫做拓扑等价(或同胚)
所以是可以利用微分, 连续,有界 等等来研究拓扑结构。 函数的微分性质。
拓扑学是研究点集与函数的拓扑性质的学科。
连续性就是函数的一个拓扑性质。
紧致性与连通性都是拓扑性质。
别如连通集的补集不连通。
但是牵涉到`X` 或它的子集的诸如大小,形状,角度,长度,面积或者体积等特性,它就不可能是拓扑性质。
不动点理论 \(f(x)=x\) 就是求不动点的过程。
线段的每一个自映射至少有一个不动点,那么对于差分方程应该有不少的不动点了。
圆到直线的每一个映射都把某对对径点映成同一个象点。 就一个就是平分问题,
薄煎饼问题¶
如果 A 与 B 是同一平面中两个有界区域,那么平面中存在一条直线,它把每个区域分成等面积的两半。 同样如果A是平面中有界区域,那未存在着两条垂直的直线,把A分成面积相等的四份。
一维是区间二维是 圆片 平面中一圆C与它的内部并集叫做一个圆片D,圆C叫做D的边界.
以及绕数,拓扑问题,现在看来都可以通过函数的性质来进行研究。
二维的主要定理¶
设 \(f:D->P\) 是从一圆片到平面的映射,C 是D 的边界圆,并设y 是平面中不在fC上的一点,如果 f|C 在点y处的围线数不为零,则 \(y\in{fD}\) 也就是存在一点 \(\exists x \in D, f(x) =y\)
例如树的年轮可以用闭区线同伦。 的函数定义。
混沌理论¶
| chaos | 数论 | 数学分析 | |
| 张量分析 | ` 复变函数 <ComplexFunction>`_ | 矩阵论 | |
| 近世代数 | 概率统计与随机过程 |
| 实变函数 | 集合理论 | 离散数学 |
– Main.GegeZhang - 08 Feb 2013
| 方均根误差 RMSe=sqrt(sum((Ti-Ai).^2)/n) | ||
| 方均跟误差函数:std(abs(x1-x0)) | x1是求得数据,x0为原始数据 |
root mean square sqrt(1/N sum((x1-x0)^2+(y1-y0)^2)) x1 和y1变动起来。 [Direct Position Determination of Multiple Radio Signals]
泛函数分析¶
主要研究无限维空间(具有各种拓扑)的结构,它间之间的映射以及映射的微积分。
See also¶
- mathoverflow 一个不错数学论坛
- 本科数学专业课程
- 数学专业的大学课程该怎么学呢?哪些课更重要?
- 将数系从复平面扩展至三维等高维数空间完全可能 在低维复杂的问题,到了高维就变的简单了
- 超越复数的三元数 ──从复平面到三维数空间
- 计算机与数学看看总些一下思路
- MIT牛人解说数学体系
- matth videio web
- 国外数学谭程
- Video lectures on Real Analysis?
- 数学之旅 上海交大
- 图像处理中的数学问题
- 群论
- 抽象代数
- 斯坦福大学公开课 :机器学习课程 这个和自己下载的应该是配套的
- 离散优化
- 图像处理的数学方法
- http://www.360doc.com/content/10/1110/22/106832_68338547.shtml 里面的高维图像处理是什么?
- 天玑学术网 看看可以快速找到方向
- 历年全国优秀博士学位论文评选结果
- Petri网 用于状态分析,工作流设计
- 科学家怎样做科研
- 运筹学石华
- 一个数学科普网站
- 我的学习经验 杨振宁
- 文化科普
- 国内建的数学科普网站
Thinking¶
数学分析,高等代数,概率论与数理统计,解析几何,常微分方程,实变函数论,复变函数,微分几何,近世代数,数论,我们学校还另外开了数学建模以及经济数学中那个叫啥来着......基本上就这些专业课了,LZ想跨过来的话个人以为数学分析和高等代数要系统的学了,特别是数学分析,没学好这个的话后继课程基本上学了也白搭,加油吧,毅力胜过一切!
– Main.GangweiLi - 18 Sep 2013
我学的是基础数学,数学分析高等代数解析几何是基础,抽象代数是高代的深入,实变函数又叫实分析是数学分析的深入,加上常微分方程和复变就可以了,拓扑和泛函是研究生的基础,努力学下就可以了~~~我感觉每门都很重要。都是整体,对了,还有微分几何,想学几何的话也是很重要的专业课。
– Main.GangweiLi - 18 Sep 2013
与其在低维上纠结的事情,放在高维的就变的简单了。最重要的那就是独立思考力。所以能够快速掌握利用计算机来进行推导。可能要真的去看看hackwell语言了。它能更高层面解决你的编程问题。
– Main.GangweiLi - 19 Sep 2013
梁伟说 图像搜索,视频图像处理现在比较火。
– Main.GegeZhang - 14 Oct 2013
行列式det的意义是什么?都有哪些用途?
– Main.GegeZhang - 16 Oct 2013
建模思路 Mathematical_optimization
- 建立目标方程
- 寻找约束条件
- 利用拉格朗日乘法与KKT来建立解方程式
- 通过求极值或者解方程来得目标条件
- 分析目标条件性质,再进一步优化计算,或者寻找简化计算
– Main.GangweiLi - 24 Feb 2014
代数¶
代数是研究数,数量,关系与结构的数学分析。 http://baike.baidu.com/view/556393.htm
数本身有数论,数量,主要就是集合论了。 关系,就是各种运算,加法乘法,再加序。 数,多数项式,矩阵。
集合+一定的运算属性 = 群,环,域,线性空间。
映射->变换->函数。
函数的定义域,值域。象。
运算律¶
结合律,交换律,分配律
群,环,域¶
对于一个集合,再加一个代数运算。
#. 群 只要非空集合,并且对一个运算 \(\circ\) ,有 \(e\) 元,就是1,即 \(e\circ=a\) 并且 \(a^{-1}=e\) 就称为 这个集合为这个运算的群。 G的代数运算满足交换率,则称为交换群。
而即1,又有倒数的就叫做群了。这些都是相对于代数运算来说的,例如满足交换律就是交换群。 对R对这两人个代数运算成为一环。 加法群也就是由0元。 (可以用来研究对称与周期性).
#. 环 对于两个代数去算,+,* 集合R为加法作成一个加群,R对乘法满足结合率,并且乘法对加法满足左右结合律。 环则是更上一层两个代数运算的系统就叫做环。
- 域 可除环就是域,也就是非零元素都要有逆元。也就是可以做除法的环就做域。
我们平时所说的定义域,值域,域就是指上面的定义的域。
- 空间 具有特定结构的集合。 http://en.wikipedia.org/wiki/Space_(mathematics)
- 而常见的结构有 http://en.wikipedia.org/wiki/Mathematical_structure。
#. 线性空间 例如只满足加法与数乘集合就叫线性空间。以及八条性质就就叫空间了。
See also¶
Thinking¶
数,多项式,矩阵的出现是为了刻画一些物理理和向何量,诸如长度,面积,空间中点的位置,平面的运动,几何变换。但是对于对称性,以及周期性的描就会发现群是最好的表达工具了。
– Main.GangweiLi - 03 Nov 2013
logistic map¶
- Logistic混沌映射 系统状态与初始值相关的,不同的初始值会导致无序
- Xn+1=Xn×μ×(1-Xn) μ∈[0,4] X∈[0,1]
See also¶
Thinking¶
feedback),把输出当作输入,不断滚动。很容易想到,反馈的结果有若干种:发散的、收敛的、周期的等等。但是我们要问一下,一共有多少种可能的运动类型?是否存在既不收敛也不发散,也不周期循环的迭代过程? 回答是肯定的。这一点至关重要,但可惜的是人们最近才普遍认识到有这种运动类型。这说的就是有界非周期运动,它与混沌有关。
– Main.GangweiLi - 19 Sep 2013
*映射*有一维映射,二维映射, 有三维吗。
– Main.GangweiLi - 19 Sep 2013
– Main.GangweiLi - 19 Sep 2013
Thinking¶
*离散与连续的区别与联系*这是很微妙的。
– Main.GangweiLi - 17 Oct 2013
– Main.GangweiLi - 17 Oct 2013
第一讲: 微积分引入的原因是:运动和 无穷, 解决方法是极限。
在那一瞬间,临时的一个点,究竟是一个固定点,是变量点
自由落体运动的平均速度是多少?
在某一点的速度是多少?
%$frac{1}{2}gt^2=frac{s(4+h)-s(4)}{h}=frac{g(4+h)^2-g(4)^2}{h} =80$%
那么无穷多个数相加是什么? 他应该怎么计算?
Introduction¶
连续,有界,收敛,单调性,极限等等可以表征函数特征或者曲线或者曲面的特征的。
可微性就是输入的变换与输出变换 的关系的一种度量的(可能是线性)。就像冲函数与阶跃函数可能不具备这些特点,也就不可微了。 其实也就是时序性,可加性的体现。也就是为什么积分符号在离散上累加和的原因。
数列最早是自然数函数,最后扩展到实数。就变成函数。再从低维到高维。
数列的极限¶
对于任意给定的E>0,可以找到正整数N,使得当m>N时,则|f(n)-a| <E. 数列的极限与前有限项没有关系。 并且有邻域(a,e). 也就是 math:|a - x | < e. 这样就可以随意放大与缩小,利用不等式。 以零为极限的变量称为无穷小量。 #. 极限的唯一性。 #. 数列的有界性 #. 数列的保序性 #. 数列的夹逼定理 数列的四则运算与与正常线性系统是一样的。
数列,级数,幂级数¶
常数项级数也就是数列,最终的结果是一个瞬间的值,也就是一个点,而函数项级数则是曲线叠加,是具有时序的。通项,与前n项和。 幂级数的收敛半径。
思路把一个函数展开级数。展成幂级数,就是泰乐级数,系数就 \(1/n!f^(n)(x0)\)
tylor series 把一个复杂函数变成一个简单我多项式来逼近。 幂级数本身也是基函数族。就是为了近似计算,其中二项展开最为精典。
三角函数与复变函数的关系就是欧拉公式。
泰乐极数就是把任一函数变成,幂级数的多项式,傅里叶级数,利用正余弦的函数基的正交性并且计算的方法,就相当于矩阵求上三角阵。然后根据精度取舍了,直流量就是只有一个量相当于列了。
傅里叶级数是用的积分,卷积也是用积分。
直接利用傅里叶级数的系数那就是傅里变换。
奇偶性还是为了研究对称性。 是不是可以高维二项式生成一个级数。
并且利用wolfram很方便。提供各种中Laurent 以及Pusieux级数。 代数体函数,不通过解方程,只通过系数来探解解空间的性质。
无穷大量¶
就像无穷小量,有严格的定义。 并且无穷大与无穷小互为导数。 一些不定式分情况而定,对于stars定理,如果 lim dx/dy=a,则lim x/y=a. 要求 x,y严格单调递增。
收敛准则¶
- 收敛数列有界,有界数列不一定收敛。(有界,单调必有收敛)
通过极限我们就可以把定量与定性分析相互的转换。例如xn>0,则xn=1+xn/(1+xn)的它的极限值就是1/2+1/2*sqrt(5) . 不需要求初始值与具体值。 可以递归公式求出极限值。两边同时求极限,然后再解方程。 可以通过求x/y求极限,来知道x/y相对于极限的速度。例如都是无穷小量,如果=1就说明两者速度基本一致。 Fibonacci 的增长率的极限是0.618.黄金数。
曲线常度,积分折线常度。 例抛物线,任一条曲线的常度,可以积分点距。曲线的曲率,长度都是公式来计算的,曲率由二阶导与一阶来计算出来。长度由曲线积分来求。原来定积分只能求面积。本质是在哪里。 平曲曲线的弧长,与空间曲线弧长都是对闭区间示对于点距求积分。见P251微积分。正是有了极限微分与积分基于不同模型才有计算。现在微分与积分基本上是不分家的。有积必有微。 在不使用微积分的情况下,还是可以使用极限再初等函数的各种变换来计算。例如圆的面积就是利用数列极限的夹逼性,利用内接与外切正多边的求得圆面积。并且极限可以直接代入方程来计算。我们简称极限方程吧。 闭区间套定理,可以证明实数不列。 子列,任何子列与原数列的收敛性是一样的。 有界数列,必须收敛子列。 无界数列,必须无穷大子列。 cancky 收敛原理,收敛充分条件,就是基本数列。
| Cancky 收敛 <=>闭区套定理 <=>确界存定理 <=> 单调有界数列收敛定理 <=>Bilenao-Weiertrass 定理 | |||
| 函数极限 | Euclid空间 | ||
Thinking¶
实数的子集就是区间,开区间,闭区间。
– Main.GangweiLi - 25 Sep 2013
y=x+esin(y) kepler方程。
– Main.GangweiLi - 25 Sep 2013
运算与数系是相关的,由自然数对于加乘的封闭性,而对于整数而减法的封闭,到有理数对除法的封闭。对于开方的封闭加入无理数,从而扩展到实数。
– Main.GangweiLi - 26 Sep 2013
用haskell与python的sympy 来计算一下。
– Main.GangweiLi - 29 Sep 2013
递归公式可以Z变换求通项公式。
– Main.GangweiLi - 02 Oct 2013
线性代数与矩阵¶
关于线性与矩阵的本质 这里已经讲的很深入了 http://www.cnblogs.com/TenosDoIt/p/3214096.html 矩阵的本质就是变换,而变换的本质就是运动。空间与集合的区别。空间就是对某种运算封闭的集合。 空间的基,空间坐标与空间的坐标系。
相似矩阵,就是对同一变换的不同描述,当然有描述好,有的描述就不好。空间基就坐标就不相关。最小的秩肯定是方阵,但是 \(mxn\) 矩阵就必然有重复像。
这些都早都是由解线性方程组发展而来,研究方程系数排列而得来的。矩阵的加法与入都是方程组的变换相关的,而矩阵的乘法,是源于换元计算而来,相当于基转换。 并且将其推广到了多维空间,以至于无限维的空间。
其实求矩阵的秩就是求其最大向量无关组,也就是基的个数。对于图像的一阶导以及二阶导,是不是可以通过行列式来直接计算,而卷积计算可以相当于矩阵的分块计算。也就是池化并不改变矩阵的性质。 当做一个矩阵操作的话,所有计算应该都是可以可逆的。来来保证信息不损失呢。 特殊值与特征方程。
特征向量就是空间的基,而特殊值就是坐标值了。 如果已经有了基就是要求特征的方程。或者说已经有矩阵,求其特征值与特征向量了。
二次型其实与SVM类似,采用换元的方程实现,旋转为标准模型来计算。例如方程的ax2+bx+c=0 只有化成 (a-x)^2 =0 时,容易求解。 http://wenku.baidu.com/view/c6aa38fd770bf78a65295491.html
伽罗互运用群的思想彻底解决了用根式求解代数方程的可能性。由些代数转变成为研究代数运算结构的科学。
并且可以用来求极值,二次型的极植就是特征值中极值。 http://www.docin.com/p-180278042.html
韦达定理,
是定义的结构,至少要有一定的序。既然是有序就至少一个二元运算。
http://www.cchere.com/thread/3038887
行列式¶
行列式就是全排列求合。并且全排列的性质,因为每一行,每一列都必须出现每一个无素中,所以对于任意一行,列的操作都相当于是对于行列式所有项进行操作。同时我们还可以进行行列式任意两列相同,或者一行或者一列全为零,那么两个行列式值为零。 在python中可以使用`numpy.linalg <http://docs.scipy.org/doc/numpy/reference/routines.linalg.html>`_ 来进行常规的计算。 行列式就是一个函数,把n阶方阵,映射为一个标量,并且 在欧几何中,有着“体积”的概念。同时可以做为圆锥曲线的判别式。在看到行列式的时候,就要想着那个函数求和形式。这样就会一目录了解了,其实就是一次多项式看到特定的规律排列起来。
cross-product 就是定义按照行列式的定义来写的,只不过它是向量表示,物理意义是四边形面积,一个线性变换的行列式的值,就知道是两个两个变换前后面积比值。
inner-product表示表示的是投影,或者是向量相关性.
行列式与空间的定向性,线性变换,正为同向,负为反像。
规范化正交基的行列式=1.
\(aug_y=(a'*a)^(-1)*a'\) ; % 最小二乘,使残差最小 \(r_n=a'*(eye(10)-a*aug_y)\) ; % 正交 最小二乘就是直接投影到正交空间。
矩阵¶
一般来说,矩阵可以直接一元函数方程。如何解非线性的二元方程。二次型就是其中一种。通过左右乘同时就可以表示一个二次方程了。对于一元函数,一个矩阵表示一组方程。而二次型,二次型而是表示一个方程。 看到行列式就应该想到那个那个遍历求和式。有点类似于内积的概念。 行列式 这个里面讲了行列式的发展史,并且与各个知识的联系。
这个是矩阵 矩阵 把这两个研究明白就行了。
现在需要的是各个知识之间的联系。而各个具体知识与再用到的时候再去研究。这也许就是整体与局部的关系。我所喜欢的应该是这种整体的关系的研究。而非具体的计算。
对行矩阵 Ax=B,我们习惯于按行与按列求法不同。尤其是按列行式的行列式。最常见的x为一个列向量,而B 也是一个列向量,而A是一个矩阵。按照列看,A就是一个线性空间的基,而x就是基的坐标值了。而b 就是一个项向量。 例如是一组点。x也是一组点大坐标了。所以坐标一般都用列向量来表示。
矩阵的kronecker积有点类似于笛卡尔积。
可以用矩阵来生成线性空间。但是矩阵本身并不是代性空间。对于Ax=0,与Ax=B,其实就是一个解空间平移的过程。
对称阵¶
Bezout矩阵,是对称阵,并且还可以找到两对应的多项式来生成。
初等变换¶
左行右列。最简单的说明,那不断乘以单位阵。可以先对单位阵进行变换,然后在左乘或者右乘了。初等方阵就相当于自然数中质数,例如一个方阵都可以一组初等方阵乘积。这个就像自然数因式分解。
相似矩阵,经过有限次初等变换的能相等的矩阵那就是相似矩阵。相似型可以用来研究二次型。也就是二次函数。任意一个给定二次型都是一个对称阵。把一个二次型化成标准型,其标准形的系数就是对称阵的特征值。
矩阵乘法的理解¶
- 按照定义,最基本的理解,那就是每一个元素都是对应的左行右列,内积之后。 在这个理解里,我们要把左边的一行当做向量,而右边的一列当一个空间向量。
- 按边的Ax=B,x的每一列与A与相乘。最后得到结果一列。这个就是一组线性组合。
- 按A的每一列与X的每一行相乘。
- 左边一行与右边一行。 就相当于一层一层的叠加。是不是那个金字塔。 1.与复合函数 以及神经网络
方程本身就是函数的隐式写法。所以方程组也就是函数组。对于一个矩阵来说,行数代表因变量的个数,而列数代表了自变量的个数。矩阵相乘的意义,就是线性变例如A=B,B=C,然后直接求A=C的过程。简单一些就是复合函数。 例如例如两个矩阵F,G.分别代表的是f,g的系数行列。那么f(g)就是F*G,而g(f)而是G*F. 右乘就是求解变量的函数。而左乘那就是外面在加了一层。例如f(g(h))那就是如何求f呢,那就是F*G*H.
而神经网络其实也就是矩阵乘法的应用。
随机mapping 可以用降维,其实降维很简单,只需要生成一个m*n的矩阵,然后直接相同。就能实现降维。只是左乘或右乘。
乘法就是一种映射变换,没有固定意义,我们用随机也达到同样的目的。当然这种随机映射的能力也就是人类的类比能力,也就是 `人类为什么能从极少量的数据中学习。<http://synchuman.baijia.baidu.com/article/273458>`_
同时降与升都在这个A中。 上三角矩阵就是利用高斯消元法 ==========================================
从而A=LU-> PA=LU使其更加通用化了,而这个P叫做置换,那就是交换其行。这个P有一些特殊的性质,每一个维空间中,它们个数是有限的,每一维都有N!个。并且其其中任何一个P的转置=P的逆。并且形成一个群。
并且在这里学明白了空间与子空间。空间是由向量而来。 集合的笛卡尔积-> 向量->空间-> 线性空间->群。 对于线性空间,要求加法与数乘。并且八大基本运算规律。这些定义一定会有零空间,与一空间。也就是与0,1.这个两个值是必然存在的。 并且二维空间的一维子空间与一维空间是不一样的。因为其向量是二维的。 对于二维空间来说,它的子空间个数也是有限的,自然,0,以及所有过原点的直线。而不是我们想像的四个象限。 对于二维空间来说,它的子空间个数也是有限的,本身,0,所有过原点平面,以及直线。 每一个矩阵都可以构杨一个空间,如何构成呢,那就是其个列向量的线性组合。
一个向量空间中,只有其Ax=0 解构子空间。 而Ax=B不能子空间,没有没有零向量。但是这些解本身又具有什么性质呢。 矩阵的秩是主元的个数,那么,是由自由变量的的个数。例如haskell解数独。
-方程组的解空间¶
一组方程组解就组成一个线性空间,所以方程组的解与+,乘应该还是方程的解。 把方程组相当做函数,齐次方程组,就是没有常数量,非齐次那就是有常数项。
线性空间其实也是线性方程组的解空间。这个线性方程组就叫做变换。
%RED% Ax=b,可以看做是Ax=0的平移,所以Ax=b的解个数取决于Ax=0有多少解。 是不是看f(x)=Ax看做一个函数呢。这样原来函数变化,就有可能变成了空间的移动。随着x的变化而化。如果这样是不是可以有f(x)=Ax^n+bx^(x-1)....这样的方程呢。这样的方程有什么意义。如果这样对于描述物体运动,会更好,现在的基本变化方程已经都可以完全用4*4来实现了。
如何利用有限的线段拟合一个区域边界。反过来如果线性相关,而这个线段首尾相接就形成封闭的区线,其实也就是x1+x2+x3+x4..=0,也就是Ax=0,因为解空间的个数,另外一个那就是现在加法可以任意方向因为有交换率。但是我们如果能要求加法是单向的,不能再交换。我们是不能找到这样一个有序了数列拟合任何区域的边界。就像圆的内接多边形,现在我可以要求多边形长度有变化,有向线段,如果规定逆时针为正,这样不就是求Ax=0就好了。利用曲线的曲率来决定向量的长度。
f(x)=A*T^n*G. f(x)是最终运动方程。 A是物体本身,T就是那个仿射变换,n代表做几次变换,而g是那因变量的各种函数,你如地球转动的角度是时间函数。这样不就是一个整个的运动方程了。那么我们只要输入每一个输入状态。例如当前这个一个原点的位置,那么整个物体的位置不就知道了。
%ENDCOLOR%
线性空间维,基,坐标 有基才会坐标,坐标是一维的,有了基就可以事情简化为一维的运算。 秩是向量的最大无关组,秩也代表了可以线性方程组可以多个主元。也就相当于基的维数。而自由变量代表了解决空间的维数。
二阶导数组成一个海森矩阵。
Ax=b,我们看做一个函数,而例如f=Ax是函数的象公间,所以每b都是A的各列的线性组合。所以这个方程有解前提那是。b是A列空间一个列的线性组合。其线性组合另一个空间,并且这个空间维等+加上原空间的维数=整个空间维数。空间的最大维数是什么呢。与集合的势是什么关系。 零空间就是齐次方程组的解空间。null space 也正好是其正交补补集。也就是求f=0的值,
四个基本子空间,那就是左右零空间,与行空间与列空间。
矩阵空间,秩1矩阵和小世界图¶
秩1的矩阵是不是可以用压缩数据。如果发现一个矩阵秩为1,就可以直接使用,一行一列,就保存其全部信息。那么一幅的图像秩一般会是多大呢。 并且在numpy,有特殊的支持,那就是broadcast方式,np.ogrid正是为产生这各矩阵最简单的方法,例就是那乘法表的实现最简单。 对于矩阵直接使用reduce操作。在函数矩阵函数的时候这些就会非常的方便。 注意numpy中array 是针对向量组的,numpy的matrix才是针对矩阵的。 小世界图就是六度空间。 #. 原创–秩为1的矩阵相关性质
正交向量与子空间与子空间投影¶
Ax=0就得出它的零空间与Ax的空间正交的,并且两者维数是相加等空间维数,所以两个空间正交,也叫做正交补。Ax=b变成f=Ax的话,那就f值就一个由A的列生成向量空间。 投影的过程,也就是扔掉了Ax=0的那部分,而留下了Ax=B的那一部分。投影指的一个空间的向量在子空间的投影。如果在全空间的投影,那么投影矩阵就成了单位阵,并且误差投影矩阵就变成了0向量。只是一个子空间上投影。那么其误差就一定在子空间的正交空间中。并且误差投影+投影矩阵=单位阵。这也是必然的。 P=aaT/aTa 在解Ax=b,时无解时,取一个近视解,b取在A 上的投影,熏直量就是误差。误差最小是求投影。P=A(ATA)-1AT, 通过通过一般二维的投影提出了高维空间的投影问 并且P^的平方=P,
正投影指的投影方向与投影平面是垂直的,而斜投影而非垂直的,相当于把投影平面当做旋转,然后再投影。斜投影=错切+正投影,那如果投影面是区面怎么办,例如是一个球面呢。会有什么性质与效果呢。还有那就是`曲线曲面投影 <http://wenku.baidu.com/view/bf2fe54633687e21af45a964.html>`_ 这个就要用到矩阵函数了吧。 斜投影不仅要指定投影平面,还要指定投影方向。具体见快盘斜投影的论文。
最小二乘 算法
通过子空间投影误差矩阵,通过代性代数求正交可以快速得到,也可以通过微积分求偏导极值得到参数值是一样的过程。以前一直感觉最小二乘的神秘,现在无非二次多元多项式求偏导。求方程组的解而己。
矩阵求导¶
现在明白了矩阵求导基本的就是jacobian 行列式, 从这个角度理解,就比较容易理解求导是什么了。 一个 .. math:: m times 1$% 的向量对一个 .. math:: n times 1 的向量求导,雅克比矩阵就是%$ m times n, 我们实际上分析的时候都是基于jacobian行列式的。
<img src=”%ATTACHURLPATH%/leastSquare.JPG” alt=”leastSquare.JPG” width=‘563’ height=‘435’ />
See also¶
- 幂等矩阵 idempotent matrix
- 埃尔米特矩阵 Hermitian matrix 就是转置+共轭。
- Moore–Penrose 广义逆矩阵
- 向量的定义 具有大小与方向
- 向量与矩阵的关系
- How to perform non-linear optimization with scipy/numpy or sympy? leastquare
- scipy中的优化
- 计算数学主要研究方向
- sympy 中支持 matrix Derivative
Thinking¶
*SVD分解*左右特征值,西矩阵。西矩阵是复数=实数的正交阵。
– Main.GangweiLi - 15 Oct 2013
`奇异阵 <http://stackoverflow.com/questions/10326015/singular-matrix-issue-with-numpy>`_ 无逆,且一个行列式Det为0 并且为numpy.linalg心专门的线性代数的包,例如求rank,det等。注意求秩不直接使用matrix中那个就是返回的是维数。
– Main.GangweiLi - 16 Oct 2013
*初等方阵相当于质数*任何一个可逆方阵可都示有限个初等方阵的乘积。
– Main.GangweiLi - 17 Oct 2013
我感觉行列式和cross-product仍旧联系不起来?
– Main.GegeZhang - 20 Oct 2013
现在明白为什么要一个矩阵要乘以的转置 这个是为了解决了Ax=B的在无解的情况下,找到一个最优解。例如我们需要三个参数来建立一个方程,来求解一量。但是我们为了测量的精确,我们N组数据,这就形成了N*3的矩阵。然后,我们不知道哪一组方程是不好的,直接把它扔掉了。我们需要的基于这些值得到一个最优解。如何来得到,在方程的两边同乘以它的转置,至于是左乘还是右乘。就要看你是N*N,还是变成3*3了。并且这是一个更好的矩阵。并且这个转置矩阵秩与原来是一样的。所以取得一大组数据之后。第一步删除重复的,然后删除线性的相关。只留下线性无关的。一个向量组的秩与是等于它的维数的。[[1,2,3],[2,4,6]] 这个只是一维的。 那就有一个问题,矩阵的秩区分行与列吗。应该不区分吧?然后再乘以转置变成一个更好的矩阵。
– Main.GangweiLi - 21 Oct 2013
子空间 一个子空间的维数与正交的子空间,它们的维数之和必然要等于这个空间的维数。例一个一根直线是一维的,而法平面就是二维。这样在三维的空间。它们才是正交的。另外一个空间的子空间,是指的其一个划分呢,还是只是其低层的子空间。
– Main.GangweiLi - 21 Oct 2013
点线面 以及整个数域用集合论以空间来研究。它们属于哪一部分。
– Main.GangweiLi - 21 Oct 2013
相关=平行
– Main.GangweiLi - 21 Oct 2013
– Main.GangweiLi - 21 Oct 2013
图 用列代表结点,而行代表边,起点用-1,终点用1,无关用零。这样形成矩阵,那如何表达权重值呢,结点数-边数+环数=1
– Main.GangweiLi - 27 Oct 2013
矩阵已经看到17张了。
– Main.GangweiLi - 27 Oct 2013
sympy 中矩阵推导好像不太靠谱
– Main.GegeZhang - 04 Dec 2013
Jacobian 就是向量vector求导,有什么意思
– Main.GegeZhang - 04 Dec 2013
对于向量B=[rx,ry,rz]‘和反对称矩阵R= [0,-rz ry; rz,0,-rx;-ry,rx,0],
– Main.GegeZhang - 16 Dec 2013
- Introduction
数相对于运算而来的,由人类最初的记数开始有自然数加法,随着数量的加大就有乘法,对于自然数是封闭的。往后由于分配问题引入除法进而引入小数,再从面积引入乘方与开方。当然另外一些那就是数列。数列就是自然数集的上函数。并且很多在实数集上性质是可以转到自然数集的。 %RED% 既然是函数,我们就要研究函数的一般性质在自然数上体现,直线方程的截距式就是同余式的形式。而同余理论本身也是周性的体现。这里只用到这种取模运算。这当然也可以是别的运算。 但是前提那就是多顶式要具有常数项,它的齐次解空间就会有周期性。例如y=sin(ax+b)所以这个周期就是a,而值就是b,而这个正是周期与向位的关系。 所以多项式是不是具有常数项这是一个很关键的性质。最简单那就是说明,过不过零点。如果不过零点,那我们利用自然数同余理论来解析了。 如果具有常数项就意味着 .. math:: F(0)ne 0不过零点,意味着必有常数项。 %ENDCOLOR% + 形数 与素数 ===================
形数与形是有连系的,素数是只能线来表示,形数是可以用形状表示,例如三角形数,五角形数,可以说素数是一维的。 形数与素数是相对,素数就只能是一条线了,而形数就可以形成二维形状,最简单的矩形。当然对于它们还可以再细分。 形数 下面可以有三角形数,就是自然数n项公式。并且都是二次的,1/2k(n**2-n)-n**2+2n. 这个是通项公式。
还有一个特别的玩法,那就是幻方与数独。那就是任意的数的平方都可以是一个幻方。并且幻和。1...n**2的和,可以得到幻各s=1/2(n^2+1)n #. ACM之幻方矩阵 #. 幻方构造(三) 通过利用方阵求逆相求数独。例如3x3. 但是遇到奇异阵的问题,其行列值为0,这样其就没有逆。 另外是不是可以通过haskell直接生成一个呢,例如一个九维的矩阵,就像写勾股数一样。
对于素数也是有各种各样的素数的
| 费马素数 |
现在还没有找到一个完整的`素数公式 <http://zh.wikipedia.org/wiki/%E7%B4%A0%E6%95%B0%E5%85%AC%E5%BC%8F>`_ 如果像超越数找到这个公式呢。并且`个数与分布 <http://www.baike.com/wiki/%E7%B4%A0%E6%95%B0%E5%88%86%E5%B8%83>`_
%RED% 素数就像线性空间的基,因为所的整数可以表示成一系列素数成积再加同余,就构成了线性空间的基本要素那加法与数乘并且线性总和功能,其表现形式就是多项式。
- 有了这些计算因子的个数可以通过排列组合来得到。
- 最大公约数与最小公倍数,公约数与公倍数个数我们可以很容易的得到了。就像方程的整数解空间的问题解决了一半了。因为了有了这个素数基。
- 除数的个数都可以通过这个变成了排列组合问题。 $ 极大合数: 如果所有比它小的数的除数个数都比它的除数个数少。 $ 完全数: 它等于所有除数之和
- 进一步
- 能不把这个当做素数基用来替换原来直接二制存储,这样就变成变进制存储。相当于自然数小波变换。 这样加减乘除,以及其他的运算是不是更加简单了。实现了乘法与加法相互快速转换,并且除法与余数的计算也大大简化了。
- 额外用一个素数表来用于数据压缩。这个需要研究这个形式与数之间的表示关系了。
%ENDCOLOR% 最大公约数与最小公倍数 =================================
正是由于 .. math:: frac{p}{q} ,p,q互质把p,q按照从小最大顺序排列,则所有的有理数是可列的。正好也就说明两个有理数之间是有间隙的。并且任一公因数d一定整除最大公因数d0.并且缩写为gcd.互质数是那就是两者只有1这个公因数。互质数的乘积是一个平方数。 最大整除 .. math:: q=[frac{a}{b} ] , b=qa + r
+毕达哥拉斯问题¶
已经直角一边,去求另外两边。一个简单的 .. math:: z^2=x^2+y^2,这里不再是简单的方程求解,还有一些逻辑推理,例如要求x,y,z都是自然数,通过这些隐性的条件我们就可以得到一个解空间,并且这个解空间里的,解的个数可能是有限。所以以后遇到一个问题,不能简单的说有没有解,而应该要知道这个解空间要具有什么样的性质。
记数法¶
各种中进制的记数,最早都源于人类的生活,特别是十进制,是由于人的手指数,而20进制,而是手脚并用了,进制在往后那就是各种编码理论了,例如最常见那就是8421编码,2421编码。同时能否利用素数进行变成编码,因为中间只会缺少一些另外一些素数。因为素数是不能分解进行相互表示的,就像空间的基一样,它们是正交的。 -同余数 ==========
同余数从而形式看就是一个直线方程的截距式表示 .. math:: y=ax+b.同余数很在同一直线上。如果表示的a表示的进制,那么b就代表示这个数的个数,同余数具有相同的尾数。并且同余还有向等式一样的各种应用。并且同余数两边都是可以相以相互加减乘除的。 当我们需要解决整除的问题的时候,我们就需要来一下同余式知识。例如
$ 费马小定理:
例如我们中学所学弃九法,同余理论应用。例如模9或者模99的误差。当然日期的星期数,日历那些如何来排都是可以用同余理论来解决的。 例如日期的星期数就是模7余数。 其实同余理论就是周期性理论在自然数中体现。星期数的计算这里讲的非常的明白。
以及各种循环比赛的程序表,都是可以同余理论来解决的。
另一个应用那就是检测其是素数,还是合数。 See also ========
- flint 数论库
- 素数与音乐 这里讲为什么素数这么有意思,并且给出hackell的代码。
- 勾股定理,以及产生方法 hackell一行搞定
- 丟番圖方程 不定方程的整数解 不正式函数的隐式表达。不是可以计算这种方法计算出曲线的图形。利用笛卡尔基来列举就会非常简单。特别适合屏幕上点,因为其必然是一个整数值。
- 对代数学的发展起了重要作用的丢番
- 数学博览錧 可以看看数学的发展史
- 同余数
- 数论 总评的文章
- 交换环
- 素数与加密
Thinking¶
对于数论严究,最基本的就是那些基本数列 例如奇数列等于n顶的平方和,可以由求和公式给出。
– Main.GangweiLi - 23 Sep 2013
形数 与素数 数与形是有连系的,素数是只能线来表示,形数是可以用形状表示,例如三角形数,五角形数,可以说素数是一维的。
– Main.GangweiLi - 27 Sep 2013
不定方程就是函数的隐式表示,如何函数图形,利用列举法,例如图像的尺寸,然后逐点代入就行。利用笛卡尔积再加下过滤条件就可以得到需要的值了。利用haskell会超简单。
– Main.GangweiLi - 27 Sep 2013
看来素数还是很多性质,我们在上学的时候,只学习了其最无味的定义。所以应该让小孩把这些数论的东东都学习一样。并且可以利用计算机去证明。x^n+y^n=z^n 对于n>2是不成立的,这个是费马猜想,都是由丢番图的不定方程组的正整数解来组成的。
– Main.GangweiLi - 28 Sep 2013
zeta function,L-series 在sympy.mpmath中都有。在总结数论的时候都可以拿来直接使用。
– Main.GangweiLi - 03 Oct 2013
代数数与超越数 整系数代数方程的根。超越数正相反,所以为什么PI,E这些数在正常的方程中我们计算出不这些值来。但是什么时候我们才会用到这些值呢。
– Main.GangweiLi - 27 Oct 2013
– Main.GangweiLi - 31 Oct 2013
本原三角形,也就是三边没有公因数。
– Main.GangweiLi - 31 Oct 2013
#. opengl 投影变换,从3D到2D的转换,就是相机模型 把这两个放在一起,就会明白近端与远端的关系,其实就是一个物距与像距之间了。同时都是opengl都是右乘矩阵。 See also ========
思考¶
定义¶
冲过把长度与面积,体积的统一,就那是连乘性。每个点的各个坐标相减后相乘就得到这个值。
性质¶
四则运算¶
交,并,补,差还是可测。这些结论,对于有限次的四则运算都是成立的。
常见可测集¶
任何区间I都是可测集且同mI=|I|. 康托集的长度为零,但是又实由一一对应。
Thinking¶
传统的方法是积分,是从x分割,按照对称性也应该可以从y轴进行分割积分。实变函数主要也是从这个方向入手研究的。先把值域的范围找出来。然后分割。这就有一个问题,如果来计算函数的宽度的问题。例如y轴来看。那是不是可以当做反函数的积分。
– Main.GangweiLi - 04 Oct 2013
youku中有实变函数的许风的讲座。 可测函数相当于黎曼积分的连续与一致连续。
– Main.GangweiLi - 04 Oct 2013
康托集,最后剩下就是分割点,这些点组成的集合,就是康托点。并且小数来分示这种分割。
– Main.GangweiLi - 12 Oct 2013
点集间的距离 就像图论中,集合之间距离是由两集合之间距离最近两个点的距离。根据这个距离的大小。也会有一些性质。例如何两集相交,则距离为零。这也是以后计算零合是否相关的一个判定。同时现在有了个数,同时还可以集合自身常度的与大小的度量。出就是我们所说的面积,体积。
– Main.GangweiLi - 12 Oct 2013
集合之间的测量,例如一条线段是由点组成,那如何度量点的个数,因为是无限个点,就需要另一种度量。例如长度。例如集合自身的距离。就是所以内部点之间距离的之和。
– Main.GangweiLi - 12 Oct 2013
连续从元素的连续到集合的连续 例如康托集就是一个分段连续的典型。
– Main.GangweiLi - 12 Oct 2013
内测度与外测度类似于,左连续与右连续。不过集合,那就是从内部切分,另外一种是外在切分。内测度相当圆内最大内接圆,外测度那就是最小正切多边形。
– Main.GangweiLi - 12 Oct 2013
依测度收敛 就是指两个函数的差值,极限为零。随着其中n趋向于无穷大时。这个其实就是不正是无穷极数的用法吗。
– Main.GangweiLi - 13 Oct 2013
依测度收敛与处处收敛函数的关系。
– Main.GangweiLi - 13 Oct 2013
下积分=上积分的时候,就是可以有积分。
– Main.GangweiLi - 13 Oct 2013
lebeg积分就是分段积,只要是有限的,就有有限加加性。那么无穷极数的积分。会是怎么样呢。
– Main.GangweiLi - 13 Oct 2013
有界可测就是可积的。
– Main.GangweiLi - 13 Oct 2013
无界函数的积分是当做有界函数求极限来得到的。
– Main.GangweiLi - 13 Oct 2013
笛卡尔乘积的截面
– Main.GangweiLi - 13 Oct 2013
–
独立和相关什么关系?什么原因?
– Main.GegeZhang - 22 Oct 2013
See also¶
Thinking¶
对于场论,例如各个点的方程如何示。光在每一个点上切线,法线,光强,以及颜色,以加重力,以及质量。如何同时这些东西同时放在一个方程里来表示呢。就是张量。张量就相当于编程里的结构体,类的。把一个类直接当做变量。进行运算。当然以后并行计算起来后,可能就会这样的计算模型,与对应的计算机语言。
张量是就是多维矩阵,他一般也是通过HOSVD来分解的,分解后包括特征向量和特征值,特征向量满足相互正交,特征值也满足相互正交, 当特征值想superdiag 时,Tucker分解可以表示为CP分解或平行因子。
但是张量的1-rank还理解不太清楚。
– Main.GangweiLi - 30 Sep 2013
张量分解,特征向量的个数是维数相 关的。简化矩阵来计算的。
– Main.GangweiLi - 15 Oct 2013
张量特征值,不再像矩阵的对角阵。
– Main.GangweiLi - 15 Oct 2013
平行因子是张量的一种特殊形式。
– Main.GangweiLi - 15 Oct 2013
张量的秩,是可以多种。张量本身秩,分解的秩。
– Main.GangweiLi - 15 Oct 2013
n 模式积 有什么作用?
– Main.GegeZhang - 15 Oct 2013
任何东西都可以通过张量来表示,零阶张量,重量,温度,质量密度,一阶张量,力,速度,二阶张量以上我就不知道是什么了。 张量就是求和? 正交的时候就可以简写
– Main.GegeZhang - 17 Oct 2013
高维斜投影方法,是不是有做的空间?
– Main.GegeZhang - 04 Nov 2013
斜投影中是不是有更好的方法?
– Main.GegeZhang - 04 Nov 2013
张量的产生,是为进一步对坐标空间的大一统,以前的坐标都是相对坐标系的值,而用张量可以把参考系也包含进去,就相当于绝对的值。 在编程上相当于一个对象,多种形式。就像numpy中array一样,你可以不断的reshape,但是只读取方式的变化,而数据本身是没有变化的。 其实在实现上也很简单,就相当于一个数据结构对象化,多添加一些get/set.这样来隔离对象的不同。
https://www.zhihu.com/question/20695804, 在编程不断的抽象与隔离来实现大一统,而在数学上也是同样的道理。同时用张量还能表达复杂的数据结构例如结构嵌套。
统计推倒¶
PMF: 离散概率密度函数 CDF: 离散概率密度函数的积分形式 PDF: 连续概率密度函数
Normal inverse Wishart distribution¶
它是是多变量正态分布的共轭先验。
假定:
假设存在一个多变量正态分布,期望为 \(\mu_0\), 方差为 \(\frac{1}{\lambda}\Sigma\) , 其中
服从inverse Wishart distribution,那么 \((\mu,\Sigma)\) 的联合概率密度函数服从:
这里 \(\Phi \in R^{D\times D}\) 是一个逆尺度矩阵。
Gamma分布¶
Gamma 分布在概率统计中频繁现身,众多的统计分布,包括常见的统计学三大分布(t分布, \(\chi^2\), F分布)、Beta分布、Dirichlet分布的密度公式中都有Gamma的身影,当然最直接的概率分布是直接由Gamma函数变换得到的Gamma分布。对Gamma 函数的定义做一个变形,就得到如下式子:
取积分中的函数作为概率密度,就得到形式简单的Gamma分布的概率密度.
把 \(x= \beta t\) 代入,得到:
其中 \(\alpha\) 称为 shape parameter, 主要决定了分布曲线的形状, 而 \(\beta\) 称为 rate parameter 或者 inverse scale parameter ( \(\frac{1}{\beta}\) 称为 scale parameter), 主要决定曲线有多陡。
Gamma 分布的迷人之处¶
Gamma 分布与Poisson 分布、 Poisson 过程发生这密切的关系。参数为 \(\lambda\) 的Poisson分布概率可以表示为:
在Gamma分布的密度中取 \(\alpha = k+1\) 得到:
t分布¶
t分布是从正态分布而来的,但是在实际工作中, \(\sigma\) 往往是未知的,常用s作为 \(\sigma\) 的估计值,为了与u变换做区别,称为t变换,称为统计t值的分布称为t分布。
从均值为L,方差为 \(R^2\) 的正态总体中抽取容量为n的一个样本,其样本平均数 \(\bar x\) 服从均值为L、方差为 \(R^2/n\) 的正态分布,因此:
但是总体方差 \(R^2/n\) 是未知的,只能使用 \(s^2/n\): 代替,如果n很大, \(s^2/n\): 就是 \(s^2/n\): 的一个较好的估计量, \(\frac{\bar x -\mu}{s/\sqrt{n}}\) 仍然是一个标准的正态分布;
如果n较小, \(s^2/n\) 与 \(s^2/n\) 的差异较大,因此统计量 \(\frac{\bar x -\mu}{s/\sqrt{n}}\) 就不再是一个标准正态分布,而是服从t分布。
t分布式检验一个样本平均数与一个已知的总体平均数的差异是否明显。t分布检验统计量为:
See also¶
- 随机过程-简版 用打电话把随机过程给讲明白了
- 随机过程 定义讲的不错
Thinking¶
随机从何而来因果论 如果是随机就是否定因果论。其实二者是统一的,随机就是还没有发现的因果关系。为什么宙宇飞船都精确的控制,而一场球赛却不能知道结果呢,这个过程有什么难度,区别就在于飞船的每一个动作都可以精确的控制,而足球做不到精确的控制。
人们做错了事情的时候,都会找到原因,而不会归因于随机吧。 人能够走多远,取决于你明天要做什么,如果已经知道你明天要做什么,就会知道明天能走多远。首先要知道你明天要干做什么。然后才能决定明天能够走多远。
先验概率与后验概率区别在哪里,就在于未知因素减少。如果未知因素没有改变,就会存在先验与后验的问题。这也就解决了为什么大部分人炒股会赔的原因。那就是随机论来说的,那些专家更容易赚呢,为什么庄家赚的最多,源于他的未知因素最少。当然庄家也会有未知因素,例如大环境等等,所以他们也可能会赔。如果想赚钱就要解决这些问题。解决这些问题你就胜券在握了。
就像金属制作一样,现在我们掌握原理就是一个必然的东东,而在古代不知道的情况下那就只能自然条件来得到了。 所以遇到一个事情,成功胜算,就在于对于未知因素的多与少。如果不能知道,就要能快速反应。
自相关与协方差为什么是卷积 卷积本质就是循环遍历,例如每组元素之间的关系影响是怎么的,其本质就一个简单的干法每两个元素之间做乘加运算。然后这个值来判断两组数据之间的相关性。加乘其实就是线性运算。如果这两个运算给换掉呢,例如用指数加乘计算的结果会是怎么样的。所谓的分类两组数据之间的相关性。其实也就是相关系数的计算方法的问题。用线性运算的卷积。如果采用非线性卷积呢。
卷积的本质就是要做穷举的加乘运算。
伯努利大数定律是契比谢夫不等式的简单推论。契比谢夫不等式是可以用来预测当期望与方差知道的情况下 。
等式与不等式之间 转换用极限以及KTT条件
伯努利在结束<推测术>时就其结果的意义 作了如下的表述:如果我们能把一切事件永恒地观察下去,则我们终将发现,世间的一切事物都受到因果律的支配,而我们注定会在种种极其纷纭杂乱的事象中认识到某种必然。
伯努利在趋近于极限的情况下,也就是求极限的时候就是正态了。二项分布的期望与方差,并且与次数之间的关系是什么。 正态分布就是方差的分布图,只是做一个转换而己其本质就在 .. math:: f(x)=(x-mu)^2/sigma^2 二项分布期望以及方差以及变化情况,以及期望与方差的比值是怎么样的, 各种分布在解决什么问题,那就是概率与统计之间的关系。所谓的各种分布就是为解决统计与概率之间关系。正态分布其本质就是方差分布的变形而己。
用频率含估计概率的精度 ,大致上是与试验次数N的平方根成比例的。这个要用到极限以及收敛速度的问题。就像用无穷极数要保证计算的精度的问题一样,当然极数越短计算越简单。但是要根据误差取得这个值。见 P43 快盘/math/陈希孺-数理统计学简史.pdf 这个也就解决确定性不可知因数控制关系了。对于非常复杂的计算,能否用无穷极数来简化计算,但是又需要多少极,来保证达到要求的精度。也就是PCA算法,到底留多少主分量呢。
误差分析与收敛速度。 这个也就是为什么极限经常要那个不等式无穷小来得到在N的意义了。
阶乘的级数计算 会用到 .. math:: pi 斯特靈公式
- 最小二乘*
先验分布+样本信息=后验分布
切比雪夫大数定理¶
设 \(x_1, x_2,...,x_N\) 是一列两个量不相关的随机变量,他们的期望和方差为 \(E(x_k)\) 和 \(D(x_k)\). 若存在常数C使得:D(x_k)leq C(k=1,2,...,N)
对于任意小的整数 \(\varepsilon\), 满足:
该公式表明,随着样本容量n的增加,样本平均数接近于总体平均数,从而为统计推断中依旧样本平均数估计总体平均数提供了理论依据。
中心极限定理¶
假设随机变量 :\(x_1, x_2,...,x_N\) 相互独立,具有相同的分布,\(E(X_k)=\mu, D(x_k)=\sigma^2 >0\), 记:
那么从
优化理论¶
梯度下降法原理:梯度方向是沿着曲线上升变化最快的,因此对于最小化问题,使用负梯度方向则能够找到最优点。怎样保证这一步和下一步的梯度是正交的。但是具体怎样推倒:
首先函数式利用泰勒展开式,
我们对于最小值问题,n维空间的一个点移动到另一点之后,目标函数的改变情况,因此写出代表最终的目标函数的数学表达式:
其中 \(x_k\) 代表第k个点的自变量(一个向量)。d是一个单位向量,即|d|=1. \(\alpha\) 是步长, \(g_k^T\) 表示目标函数在 \(x_k\) 这一点的梯度。
在上式中要使得(1)式样取得最小,应使 \(g_k^T d\) 取得最小,因此只有也就是d取 \(-g_k\) 时,下降速度最快,这就是最速下降法的由来。
http://www.codelast.com/?p=2573
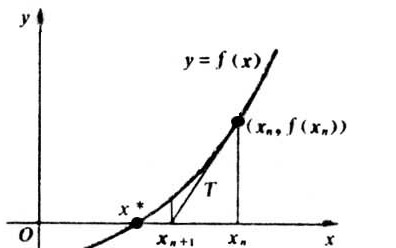
根据泰勒公式,在 \(x_0\) 处一阶展开,得到:
求解方程f(x)=0,即 \(f(x_0)+(x-x_0)*f^{\prime}(x_0)=0\),求解得到:
Note
从这个看出,后一个位置的x可以由前一个位置的x_0迭代而产生,于是迭代的想法就自然了。
进而可以推导出:
(这里的和最终的梯度下降法怎样推倒?) 通过这个式子,得到这个式子在 \((x\star)=0\) 的时候收敛,整个过程如下:
牛顿法:
相比梯度下降法速度更快。 然后又将了GLM,说明最小二乘和 logistic 回归都是GLM 指数分布的特殊情况。是不是我们现在的所有问题都是指数分布?主要是通过把某个问题划归为某个分布,然后求出期望:math:mu ,从而得到h(x)函数。
牛顿法:
把式子写为二阶形式,得到:
这个式子是成立的,当且仅当 \(\bigtriangleup x\) 无限地趋近于0,此时上式等价于:
求解得到:
得到迭代公式:
一般认为牛顿法可以利用到曲线本身的信息,比梯度下降法更容易收敛(迭代更少次数),如下图是一个最小化一个目标方程的例子,红色曲线是利用牛顿法迭代求解,绿色曲线是利用梯度下降法求解。
从这个角度来讲,梯度下降法,只使用一阶信息,相当于使用基于平面的优化,而牛顿法使用二阶信息,相当于基于曲面的优化。
最优化问题中,牛顿法为什么比梯度下降法求解需要的迭代次数更少? http://www.zhihu.com/question/19723347
http://www.codelast.com/?p=2573
Note
通过牛顿法的代入发现,最后这里使用最小值等于 \(-1/2g_k^TG_kg_k\), 这里是不是只要G_k 是凸问题,就能够得到一定能够求解到最小值。